A novel model for event ticket sales

This is going to be short. Recently I have been rewatching the comdy series The Games, mostly created by John Clarke, master of satirical comedy:

One of the episodes deals with a scandal that broke during the filming of the series: tickets were secretly sold to the rich at extraordinary prices when they were supposed to be allocated on a first-come-first-served basis. This also put me in mind of the Athens Olympics when the stands were virtually empty because people didn't buy the tickets. Same thing happened in Beijing, although the reason there was less clear.

I have a solution for this type of issue and I don't think I'm giving anything away when is say that the core of the idea rhymes with "tree kark-it". That's right: I want people to be able to pay however much or little they want to for any ticket they want.

Technically, this would be done via online auction. It would be trivial to automate such a system. I imagine a system where packages of one or several tickets for some event at some place in the arena would be made available in decreasing quantities as the event approaches. Each auction could last something like a week to give plenty of chance for those who want those tickets most at that particular time to bid for them. One could also envision a certain stock of tickets that might be sold at lottery. You could have anyone who wants them commit to pay whatever price they are sold for but the ultimate recipient and buyer to be selected by lottery. The buyer would then pay for and receive the tickets. That way you could have some tickets available at lower prices than they might be bid to at auction.

The beauty is that all tickets would be sold, since any event that most people are not interested in might have the less popular tickets going for dollars, even cents, while the most demanded tickets would be decided by the democracy of cash.

If any events organisers are desirous of paying me a small retainer I'll take it in hard currency, thanks.

Reasons why you should never buy a government bond

If there's one financial asset that should really be treated like radioactive ebola virus, it's the government bond. In the past this was not necessarily true, because way back when gold and silver were money and when the government's debts fell due it had to find the money somewhere to repay it. It had to increase taxes. This might not sound like such a fantastic thing, and you right, it's not - really all governments should run balanced budgets no matter what, but at least back then people knew what was going to happen. Of course such tax hikes in the wake of government borrowing were pretty unpopular so all monarchs were always looking for a way around that and the most effective instrument was coin clipping. Governments would reduce the precious metal content of their coins but remint them at the old valuation. When this became really popular after a while you end up with something like the late Roman Denarius with a precious metal content of 0-1%.

All this is to underline why government debt is always a bad investment. In recent times the debt of stable, high performing economies like the US, Switzerland and Germany has come under such high demand that in Switzerland the yield is now negative. In other words, the price of the bonds themselves are now so high that investors are certain to lose money, even after you consider the interest the bonds are going to pay. They are willing to lose the money because they are so afraid of any other inverstment crashing and they want something that is certain to repay their money. All of these investors are going to lose their money, or if not them, then whoever ends up with the equivalent of those bonds down the track. This is certain. Even the ever prudent Swiss or the mighty Germans will eventually end up in the same sort of tight spot Greece, the US and all the rest. Let me explain why.

First we need to examine the purpose of government debts. When a private company goes into debt it usually uses that money to invest in plant, land, resources, anything they need to grow the business and generate the profits that are going to repay the loan plus interest and leave them with plenty of new cash left over. When the government goes into debt it never does it with the intention of spending on things that will eventually repay the debt. This was originally the theory - the government would borrow from its citizens, do some large construction project like a road or a dam or whatever it might be, and as a result of this new infrastructure the economy would be more productive and the tax take would increase and allow the repayment of the original debts. Precious though this theory was to satisfy the general populace that they wouldn't suffer a burden of extra taxes later to make up for it this is not how it has ever, to my knowledge, worked out. The investment was always supposed to pay itself back in taxes and even if it didn't, the bond holders had no fear because if the project turned out to be a dud they would get their money back anyway because the government could always tax the rest of the people more to make up the shortfall. However this lovely theory has never been a reality. The reasons are multiple but the chief reasons are a) if the government's idea for an investment was profitable private investors would be doing it already and b) if - and I stress, if - the government's plan actually did make the economy more productive and did increase the tax take, none of that tax was ever earmarked for the purposes of repaying the debt. It was always more tempting to spend that money straight away and worry about the bondholders when the time came. And what typically happens when it actually does come time to worry about the bondholders? Naturally the government does not actually have the money, so instead of risking the unpopularity of forcing the populace to actually pay for the stuff the goverment had bought on their behalf, it simply sells new bonds to pay off the old bonds.

Are you seeing the problem now? You see now why those bondholders were stupid to buy the bonds at all? The government's incentives always lie towards repaying old debts with new debts. That's why nearly all western governments have had a sustained increase in debt. No one ever stopped to think about the fact that these were loans and that eventually people might ask for their money back and lose faith in the government to such a degree that they would not be willing to give up any more. Everyone knows the US government is never ever going to repay their bonds, and even so investors are still giving it up for new bonds in the certain knowledge that the money ultimately won't be repaid. They simply expect that at some future date they'll be able to find another sucker to sell it to before the bottom falls out, or that the bond will fall due and they won't be trapped into buying back into America's pyramid scheme right before it all goes west. The only reason, in other words, that the bonds have any value at all right now is because the investors expect to be able to sell them or get paid back by the US government before it has to resort to devaluing the Dollar, which, by the way, it has already been doing heavily.

Greece is substantially different from the US. In the US if they really wanted to give those bond holders back their dollars they could always print some up and give everyone their full amount. Of course that would result in instant hyperinflation the minute the investors started to try to buy real stuff with that money, but their bank accounts would at least have the right number in them. In Greece they're on the Euro standard which is one of the reasons for their woes. They can't repay the bonds they've issued because the only place for those euros to come from is taxes and the only way the economy could ever sustain such a tax take is if they were brilliant exporters to the rest of the Eurozone or, failing that, to anywhere else in the world. Needless to say, they are not. As a result of this Greek bond holders (not necessarily Greeks, people holding their bonds) have already had to take a "voluntary haircut" of 74%. That means that every single person who owned a Greek bond just before the bottom fell out has lost 74% of his money and that's despite the bailouts. Spanish, Portuguese, Italian, and other bond holders are on the same road, which is why recently they've started to edge away from those bonds, resulting in a spike in long-term bond yields:
So, to recap: you should never buy a bond because no government will ever pay it back in the long term. Even if you get your money back it's at the expense of some other sucker down the line, and even if he gets his money back in nominal terms its value will be so low he'll wish he hadn't. The eventual crisis is certain to come and when it does the economy of that country is going to tank. Do you want to be partly responsible for making that government's spending possible? Do you want to wear even a millionth part of the blame for lowering the interest rate on those bonds, which kept the state spending and made the eventual collapse worse? State issued bonds are simply a deferred stealth tax - a tax that deludes people into thinking it's an investment and produces a massive crisis when people snap out of it and realise they'll never see their money again. Now that you know, if you have a conscience or any compassion for your fellow man, don't buy a government bond. Not a single one. Not ever.

Economic fallacies abound at the UN

The recent United Nations High Level Meeting on Wellbeing and Happiness has shown how widespread certain economic fallacies are among the great and the good. Of course we knew this before, but it gives me a special chill every time some high level world leader opens his or her mouth and says something like:

The GDP-led development model that compels boundless growth on a planet with limited resources no longer makes economic sense. Within its framework, there lies no solution to the economic, ecological, social and security crises that plague the world today and threaten to consume humanity.

That was the Prime Minister of Bhutan, but lots of people feel the same way. GDP, unreliable measure that it is, tells us very little about what is actually happening in the economy. The raw aggregate tells us PQ (nominal GDP: the price level multiplied by total output) from which economists and statesticians attempt to extract Q (real output or "real GDP") which is supposed to measure how much stuff is being traded in the economy.

First of all, one of the primary fallacies of modern day environmental movements is that there are limits to the size of the economy. To understand why this is a fallacy, let's think a bit about what economic growth means in real terms. Typically it means that more stuff is being traded, or that the value of the stuff being traded increases. Less valuable resources are converted into more valuable ones using energy and human ingenuity. The limiting factors that control how much value is added are a) the amount of energy available for that process and b) how ingenious the process and product are. Energy is always finite, but there are no known limits to human ingenuity. We can always make what we're making more efficiently, and we can always find a way to make it more useful. Computers are an almost perfect example of this. They keep getting cheaper and more powerful, with no end in sight. Once we reach the limits of elemental semiconductors, we'll just move on to something even faster more efficient and just better in every way. What that is remains to be seen, but graphene, optical chips and quantum computing are all watchwords for the near-computing-future.

The same reasoning applies to all things. They can always be made more cheaply, of higher quality and greater utility. That fact means there are no currently known practical upper limits to the economy. And I very much doubt there ever will be. GDP for its own sake is stupid, but if the market is allowed to function, there are no limits to GDP, no limits to personal wealth.

We also cannot run out of natural resources. Every now and again you will hear the doom-mongers say that we only have 20 years left of silver or whatever. That's nonsense. They seem to miss the fundamental fact that after silver (for example) has been mined it doesn't actually disappear, it is made into goods. We therefore cannot "run out" of it - if we ever reach a point where all practically exploitable mines have been exhausted, we will just recycle the silver we've already mined into the most useful forms. The price system will take care of that automatically. This applies to all rare resources and yes, that includes oil, coal and the rest of the non renewable energy resources. We genuinely can "run out" of them but when we do we'll just make more any way we can from raw materials using some other form of energy. It's already been done.

We desperately need an economy that serves and nurtures the wellbeing of all sentient beings on earth and human happiness that comes from living life in harmony with the natural world, with our communities and with our inner selves. We need an economy that will serve humanity, not enslave it.

If there's one sure way of making people poor, its denying them the market. Goods sold on the market are sold because they help people's wellbeing in some way. They help serve people. Whether that is a function of producing things or just being useful to people in itself, all things are sold because people want them, and people want them because they are useful. In economic parlance, they "give ease". The reason we do not live in harmony with the natural world, whatever that means, is because a) few naturally produced resources are useful in their totally natural form and b) if we did then most people would have to die, because farming is unnatural and the level of population the earth can sustain without agriculture is extremely low. Living in harmony with nature is living in slavery, because no matter how ingenious a plan it cannot be implemented without changing nature in some way. You cannot build a house without annexing some ground that could have been used by nature for plants. All of this is to say that humans are meant to be masters of nature, the Bible even says so. This does not mean that we may destroy it, of course, but we may certainly change it so that it better serves us. That's what we have been doing ever since we began to exist, and nothing will ever stop us doing it. Mastery of nature is what provides us with wellbeing in terms of medicine, easy labour, high food production, comfortable living and work spaces, pleasing entertainment. If you want to give that up and live like a savage again feel free, but don't complain if no one else does.

The idea that the economy enslaves us is, again, a common fallacy. I stated in a previous entry on money that we are not serving Mammon but other people. The very division of labour that provides such bounty would allow someone to work only a few hours a week for all the food he needs. If that same person wanted to live off nature he would be forced to work constantly just to stay alive.

Prime Minister Thinley concluded by reminding the gathering that “business as usual cannot go on and tinkering with the existing system will not do… we need a fundamental transformation”.

A fundamental transformation. Well, yes I'd like to see free markets everywhere. That would be a great fundamental transformation. Time to get the State out of the way of commerce so that resources can be exploited more efficiently. I wonder what sort of fundamental transformation he has in mind, and whether it will be popularly demanded or simply imposed by force.

Learning mathematics needn't be hard

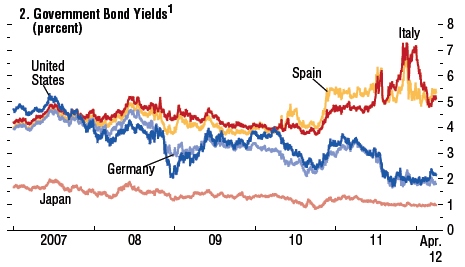
I've been mulling for a while now about the factors that make some people like maths and some people hate it, for some people it comes easily, for others every step is a struggle. I have come to believe that nearly all people are capable of mathematical thinking, but that external factors affect how well they can put this into practice.

Consider the following: a 16 year old student will be very familiar with basic addition and subtraction. What would happen if you assigned 100 problems of this very easy difficulty? Would he get a perfect score? I very much doubt that he would. I have often observed that highly capable students are prone to "silly mistakes", nearly all of which are incorrect addition or subtraction. In the past I put this down to a feeling of ease or simplicity - the student doesn't properly respect the need for vigilance in these simple matters because the difficulty is trivial. They assume they they will not make any mistakes, even though they often do and that these mistakes are just as damaging to the final answer as forgetting how to solve quadratic equations.
Recently I have broadened this conception and done a little research which has been most enlightening. Before I give you my full theory, let's consider a different problem.

The same student as before is not at all familiar with matrices. Now imagine he were asked, without much theory, but just enough to satisfy the teacher that he "should know" how to do it, to find the matrix inverse of a 3x3 matrix and multiply it by the original to produce the 3x3 identity matrix. Most people would not be able to do that even if all the correct theory were right in front of them. You must slowly be intriduced to the fundamentals of matrix multiplication, the meaning of the determinant, indentity matrix, matrix inverse and so on, and at that point he may be asked to combine all those pieces of knowlege to solve this particular problem. This is a perfect case of "too hard" - the problem is tractable but too much is expected of the student. He doesn't have the necessary framework and to ask him to develop the framework as he is answering the question will result in frustration, distraction, boredom and, if the task is difficult enough, the student will give up.

Now the third, "Goldilocks" case: the same student, having knowlege of trigonometry, is asked to determine the volume of, say, a tetrahedron in which the sides are length l. The student knows everything necessary to complete the problem, but has to apply it in a way he may not have done previously. He feels energised and confident that he can solve the problem, and does not become bored or frustrated but solves the problem flawlessly.

If you hate mathemathics the third scenario may seem remote or unrealistic, but I hope that what is to come will change your mind.

What struck me when I considered the above three situations is that it is very similar to a curve I had seen before - one to which I linked on this very blog. If you scroll down in that PDF you will see a curve that shows the relationship between speed and concentration. As you can see at low speeds performance is low, and it increases with speed up to a point, after which it declines again. The fundamental idea has been known in Psychology for about a century and is called the Yerkes-Dodson law, after the authors who developed the theory. Personally I believe that the curve should look like some sort of log-normal curve, but the essential thought is there. There is a zone of optimal stimulation or arousal (stop giggling) which produces the best performance, and movement of the stimulus either way will decrease performance. I believe the same is true for mathematics - if the problem is too easy or too hard, you won't learn much and your answers will often be wrong. If the problem is just the right difficulty, you will get the most correct answers and feel the most stimulated. You may even enjoy it. Believe it or not there are people who enjoy mathematics, and my model predicts that they will be skilled at knowing their "zone" and staying within it.

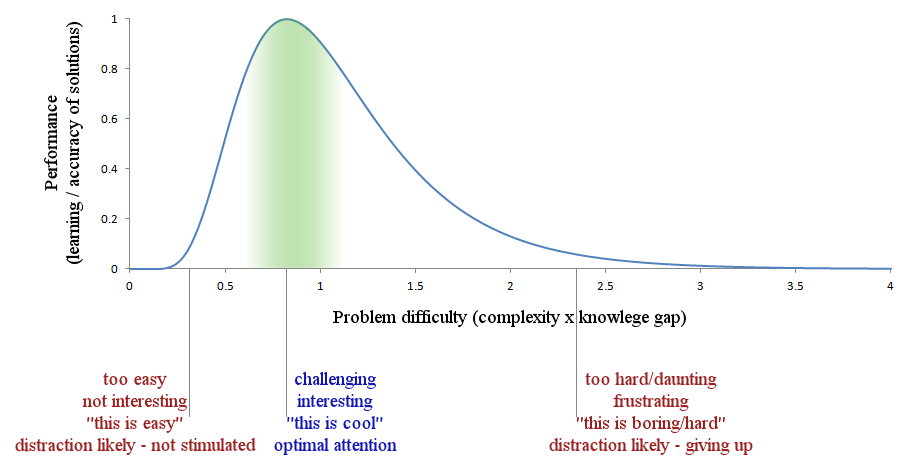
The general idea

So, now that we know this, how does it help us teach and learn mathematics? Firstly I am going to assume that the precise shape of the curve is immaterial. It is enough to know that the peak exists and that straying too far from it will impair learning.
The teacher's job, then, is to find out where the student's zone is and shepherd him in that direction. This is already practiced to a limited degree in the classroom - students who quickly grasp the current topic are placed in accelerated or advanced groups so that they don't get bored. Students who struggle with math are often placed in classes where the problems are easier. While there is some sense to this I believe it misguided. The assumption is that some students have a peak which is shifted more towards the "hard" end, and these are placed in the accelerated class, and some have a peak shifted to the "easy" end, and these are placed in the - well, let's face it - the dumbed down class.
However, this is not the teacher's only job. Current education models force the teacher to plough on with material even when significant portions of the class don't understand it. Separating the students by their ability is a bandaid fix for this situation. It would be far more beneficial if the underperforming students' peaks could be shifted to the right. I believe the way to accomplish that is not to teach them mathematics but logic and problem solving. These are mental tools essential for mathematical learning and yet few schools make any serious attempt to teach them. The results are obvious - some gifted students somehow end up with a decent logic and problem solving framework (perhaps those with high intelligence can simply work it out themselves without being taught?), and shoot ahead, while most of the others can barely add 2x + 2x.

To my mind this leads us back to Classical Education in which logic is taught before complex mathematics. Although most students cannot be redirected easily on to the different path that Classical Education takes, they can certainly be taught the basics of logic and problem solving required to learn and enjoy mathematics.